Décagone et ses propriétés géométriques expliquées

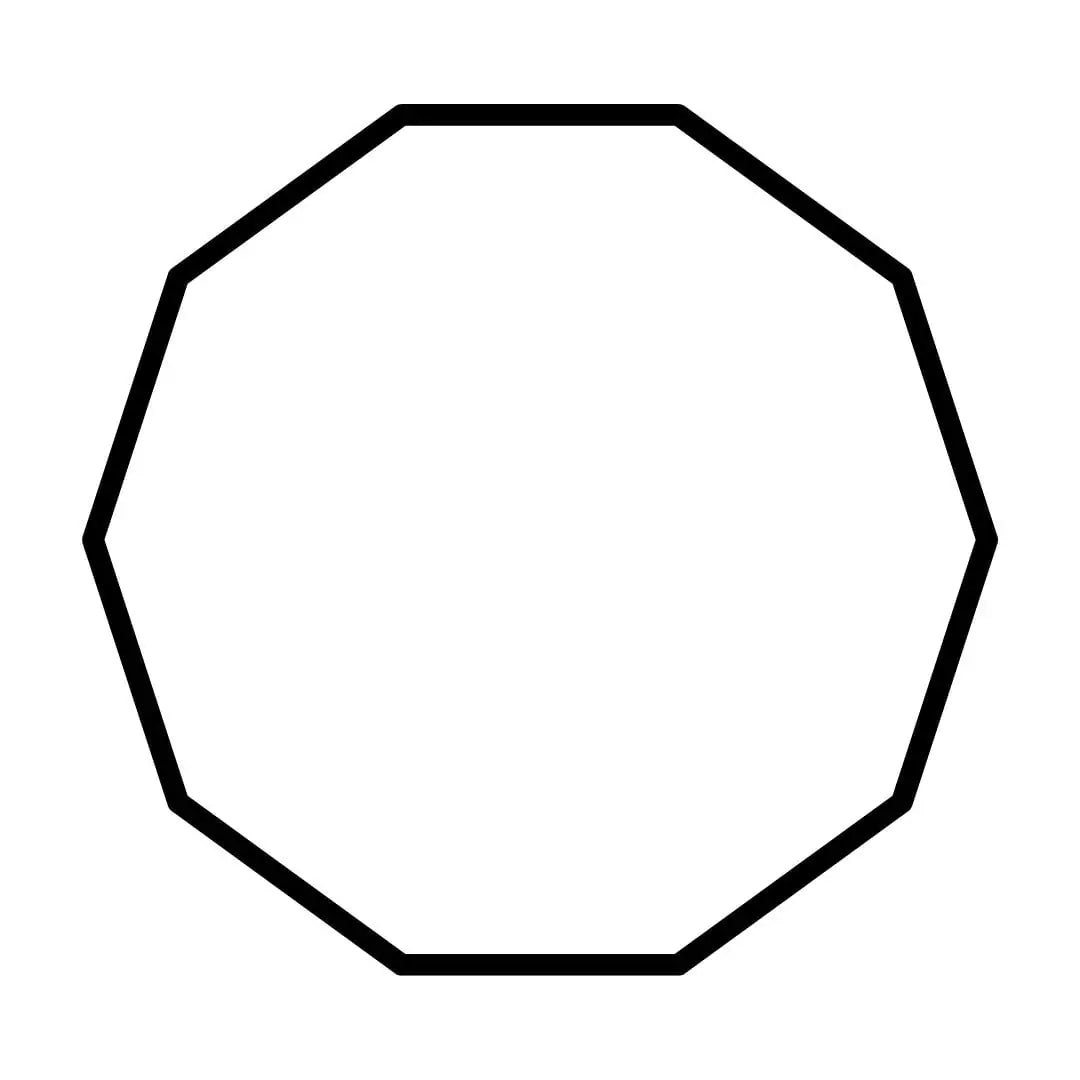
Un décagone est un polygone composé de dix côtés et dix sommets. Vous le rencontrez souvent dans la géométrie, où il sert à explorer des concepts comme les angles, la symétrie et les diagonales. Ce polygone joue également un rôle clé dans d'autres domaines, comme l'architecture et l'art, où il inspire des motifs complexes et harmonieux. Sa structure unique en fait un sujet fascinant pour les amateurs de mathématiques et de design.

Qu'est-ce qu'un décagone ?

Définition et caractéristiques principales

Un décagone est un polygone qui possède dix côtés et dix sommets. Chaque côté est une ligne droite, et les sommets sont les points où ces lignes se rejoignent. Si tous les côtés et tous les angles sont égaux, on parle d’un décagone régulier. Dans ce cas, il présente une symétrie parfaite et des propriétés géométriques intéressantes.

Tu peux aussi rencontrer des décagones irréguliers, où les côtés et les angles ne sont pas tous identiques. Ces formes apparaissent souvent dans des contextes pratiques, comme le design ou l’architecture. En géométrie, le décagone est souvent étudié pour comprendre des concepts comme les angles internes, les diagonales et les relations avec les cercles.

Différence entre décagone régulier et étoilé

Le décagone régulier est une figure simple et harmonieuse. Ses dix côtés sont de même longueur, et ses angles internes mesurent tous la même valeur. Cette forme est souvent utilisée dans les constructions géométriques et les motifs décoratifs.

En revanche, le décagone étoilé est une version plus complexe. Il est formé en prolongeant les côtés d’un décagone régulier pour créer une étoile à dix branches. Cette figure, appelée aussi "décagramme," est fascinante par sa symétrie et son esthétique. Tu la retrouves souvent dans l’art, les symboles culturels et même la géométrie sacrée.

Origine et étymologie du terme "décagone"

Le mot "décagone" vient du grec ancien. Il est composé de "déka," qui signifie "dix," et "gonos," qui signifie "angle" ou "coin." Cette origine reflète directement la structure du décagone, qui possède dix angles.

Tu peux remarquer que de nombreux termes géométriques ont des racines grecques similaires. Cela montre l’influence des mathématiciens grecs anciens, comme Euclide, sur le développement de la géométrie. Leur travail a permis de nommer et de définir des formes comme le décagone, que nous utilisons encore aujourd’hui.

Propriétés géométriques du décagone

Somme des angles internes et mesure des angles

Un décagone possède dix angles internes. Pour calculer la somme de ces angles, tu peux utiliser une formule simple :
[ \text{Somme des angles internes} = (n - 2) \times 180^\circ ]
Ici, (n) représente le nombre de côtés. Dans le cas du décagone, (n = 10). Donc, la somme des angles internes est :
[ (10 - 2) \times 180^\circ = 1440^\circ ]
Chaque angle interne d’un décagone régulier mesure la même valeur. Tu peux la trouver en divisant la somme totale par le nombre d’angles :
[ \text{Mesure d’un angle interne} = \frac{1440^\circ}{10} = 144^\circ ]
Si tu travailles avec un décagone irrégulier, les angles internes peuvent varier. Cependant, leur somme reste toujours égale à (1440^\circ).

Symétrie et axes de symétrie

Un décagone régulier est une figure hautement symétrique. Il possède dix axes de symétrie. Chaque axe passe soit par un sommet et le milieu du côté opposé, soit par deux sommets opposés. Ces axes divisent le décagone en parties égales et reflètent sa structure harmonieuse.

Tu peux aussi observer une symétrie de rotation. Si tu fais pivoter un décagone régulier autour de son centre, il revient à sa position initiale après une rotation de (36^\circ) (car (360^\circ \div 10 = 36^\circ)). Cette propriété rend le décagone utile dans les motifs répétitifs et les designs géométriques.

Relation avec le cercle circonscrit

Un décagone régulier peut être inscrit dans un cercle. Cela signifie que tous ses sommets touchent le bord du cercle. Ce cercle est appelé le cercle circonscrit. Le centre du cercle correspond également au centre du décagone.

Pour dessiner un décagone régulier inscrit, commence par tracer un cercle. Ensuite, divise le cercle en dix parties égales à l’aide d’un rapporteur ou d’un compas. Les points de division deviennent les sommets du décagone. Cette relation entre le décagone et le cercle montre l’importance des polygones dans la géométrie circulaire.

Diagonales et leurs propriétés

Les diagonales d’un décagone offrent des perspectives fascinantes en géométrie. Une diagonale est un segment de droite qui relie deux sommets non adjacents d’un polygone. Dans un décagone, ces diagonales créent des motifs complexes et symétriques, souvent utilisés dans l’art et le design.

Combien de diagonales dans un décagone ?

Pour déterminer le nombre total de diagonales dans un décagone, tu peux utiliser une formule simple :
[ \text{Nombre de diagonales} = \frac{n \times (n - 3)}{2} ]
Ici, (n) représente le nombre de côtés. Dans le cas du décagone ((n = 10)), le calcul donne :
[ \frac{10 \times (10 - 3)}{2} = 35 ]
Ainsi, un décagone possède 35 diagonales. Ces segments relient les sommets de manière unique, formant un réseau géométrique impressionnant.

Longueur des diagonales

Dans un décagone régulier, les diagonales peuvent avoir différentes longueurs. Cela dépend des sommets qu’elles relient. Par exemple, une diagonale qui relie deux sommets adjacents au sommet de départ sera plus courte qu’une diagonale qui traverse le centre du décagone. Si le décagone est inscrit dans un cercle, tu peux utiliser des relations trigonométriques pour calculer précisément ces longueurs.

Rôle des diagonales dans la symétrie

Les diagonales jouent un rôle clé dans la symétrie du décagone. Elles divisent la figure en triangles et autres formes géométriques. Ces divisions permettent d’explorer des concepts comme les axes de symétrie et les centres de rotation. En étudiant les diagonales, tu peux mieux comprendre la structure interne du décagone et ses propriétés mathématiques.

Les diagonales ne sont pas seulement des éléments géométriques. Elles sont aussi des outils pour résoudre des problèmes complexes. Par exemple, elles aident à calculer l’aire d’un polygone ou à analyser des motifs dans des figures étoilées.

Construction d'un décagone régulier

Méthode avec compas et règle

Pour construire un décagone régulier, tu n’as besoin que d’un compas et d’une règle. Cette méthode repose sur des principes géométriques simples. Elle te permet de tracer une figure précise sans outils complexes. Le compas sert à dessiner des cercles et à diviser leur circonférence en parties égales. La règle, quant à elle, t’aide à relier les points pour former les côtés du décagone.

Étapes détaillées pour une construction précise

1. Trace un cercle : Utilise ton compas pour dessiner un cercle de la taille souhaitée. Le centre du cercle sera également le centre du décagone.

2. Divise le cercle en dix parties égales : Avec le compas, mesure la longueur de l’arc correspondant à un dixième de la circonférence. Marque ces points sur le cercle.

3. Relie les points : Utilise ta règle pour relier chaque point marqué à ses voisins. Tu obtiendras ainsi les dix côtés du décagone.

4. Vérifie la régularité : Mesure les côtés et les angles pour t’assurer qu’ils sont égaux. Si nécessaire, ajuste les lignes pour corriger les petites erreurs.

Conseils pour éviter les erreurs courantes

• Ne force pas sur le compas : Une pression excessive peut déformer le cercle ou déplacer le centre. Travaille doucement pour garder une précision optimale.

• Vérifie tes mesures : Avant de relier les points, assure-toi que les distances entre eux sont égales. Cela évite les asymétries.

• Utilise un papier de bonne qualité : Un papier trop fin peut se déchirer ou se plier, ce qui rend la construction difficile.

• Prends ton temps : La précision demande de la patience. Ne te précipite pas pour éviter les erreurs.

Avec ces étapes et conseils, tu peux construire un décagone régulier parfait. Cette méthode est idéale pour apprendre les bases de la géométrie et pour créer des motifs élégants.

Applications et utilisations du décagone

Décagone en architecture et design

Le décagone joue un rôle fascinant dans l'architecture et le design. Tu peux le retrouver dans des structures modernes et historiques. Sa forme géométrique unique permet de créer des motifs harmonieux et équilibrés. Les architectes utilisent souvent le décagone pour concevoir des pavages, des dômes ou des façades. Ces éléments ajoutent une touche esthétique et symbolique aux bâtiments.

Dans le design intérieur, le décagone inspire des motifs décoratifs. Par exemple, les carreaux de sol ou les plafonds ornés de formes décagonales apportent une sensation d'élégance et de symétrie. Tu peux aussi observer cette figure dans les meubles ou les objets d'art, où elle sert à créer des compositions visuellement captivantes.

Symbolisme dans l'art et la culture

Le décagone possède une signification symbolique dans de nombreuses cultures. Tu peux le voir dans des œuvres d'art, des mosaïques ou des monuments. Sa symétrie et ses dix côtés représentent souvent l'harmonie, la perfection ou l'équilibre.

Dans certaines traditions, le décagone est associé à des concepts spirituels. Par exemple, il apparaît dans des motifs géométriques sacrés, où il symbolise l'unité entre le matériel et le spirituel. Les artistes utilisent cette forme pour transmettre des messages profonds ou pour créer des œuvres qui captivent l'œil et l'esprit.

Tu peux aussi trouver le décagone dans des symboles culturels, comme des blasons ou des emblèmes. Ces représentations montrent comment cette figure géométrique transcende les frontières entre l'art, la culture et la spiritualité.

Utilisation en mathématiques et en sciences

En mathématiques, le décagone est une figure clé pour explorer des concepts géométriques. Tu peux l'utiliser pour étudier les angles, les diagonales ou les relations avec les cercles. Les enseignants s'en servent souvent pour expliquer des notions comme la symétrie ou les transformations géométriques.

Dans les sciences, le décagone apparaît dans des domaines comme la cristallographie ou la chimie. Par exemple, certaines molécules ou structures cristallines adoptent des formes décagonales. Ces configurations permettent de mieux comprendre les propriétés des matériaux.

Tu peux aussi rencontrer le décagone dans des modèles scientifiques. Il sert à représenter des systèmes complexes ou à résoudre des problèmes liés à la symétrie. Cette polyvalence montre l'importance du décagone dans les disciplines scientifiques et éducatives.

Décagone et mathématiques avancées

Lien avec le nombre d'or

Le décagone régulier possède un lien fascinant avec le nombre d'or, souvent noté ( \phi ) (phi). Ce nombre, environ égal à 1,618, apparaît fréquemment dans la nature, l'art et les mathématiques. Dans un décagone régulier inscrit dans un cercle, le rapport entre la longueur d'une diagonale et celle d'un côté est égal au nombre d'or. Cette relation unique confère au décagone une harmonie géométrique qui le rend particulièrement attrayant dans les motifs artistiques et les constructions architecturales.

Cette connexion avec le nombre d'or montre comment le décagone dépasse la simple géométrie pour s'inscrire dans des concepts mathématiques plus profonds. Tu peux aussi retrouver cette relation dans d'autres figures géométriques, comme le pentagone ou le pentagramme.

Décagramme et figures connexes

Le décagramme est une figure étoilée formée à partir d'un décagone régulier. Pour le tracer, tu relies les sommets du décagone selon un certain intervalle, par exemple en sautant deux ou trois sommets. Cela crée une étoile à dix branches, souvent utilisée dans l'art et les motifs décoratifs.

Il existe plusieurs types de décagrammes, chacun défini par la manière dont les sommets sont connectés. Ces figures étoilées possèdent des propriétés symétriques fascinantes. Elles apparaissent dans des contextes variés, comme les mosaïques islamiques ou les symboles ésotériques.

Tu peux également explorer d'autres figures connexes, comme les polygones étoilés à moins ou plus de dix côtés. Ces formes enrichissent ta compréhension des symétries et des motifs géométriques complexes.

Importance dans la géométrie algébrique

En géométrie algébrique, le décagone joue un rôle important dans l'étude des courbes et des surfaces. Par exemple, tu peux utiliser un décagone régulier pour construire des polygones inscrits ou circonscrits, qui servent à analyser des équations algébriques complexes.

Les sommets du décagone peuvent aussi représenter des points sur une courbe algébrique. Ces points permettent d'explorer des concepts comme les intersections ou les symétries. En combinant la géométrie et l'algèbre, tu peux résoudre des problèmes mathématiques avancés et découvrir des propriétés cachées des figures géométriques.

Cette importance montre que le décagone n'est pas seulement une figure esthétique. Il constitue aussi un outil puissant pour explorer des concepts mathématiques avancés.

Décagone et géométrie sacrée

Signification symbolique du décagone

Le décagone, avec ses dix côtés, représente souvent l'harmonie et la complétude. Dans de nombreuses traditions, le chiffre dix symbolise l'unité entre le matériel et le spirituel. Chaque côté du décagone peut être vu comme une étape vers l'équilibre parfait. Cette figure géométrique incarne également la stabilité, grâce à sa symétrie et à sa structure régulière.

Tu peux remarquer que le décagone est utilisé dans des contextes spirituels pour évoquer des concepts universels. Par exemple, il est parfois associé aux dix directions cardinales dans certaines philosophies, symbolisant une connexion avec l'univers tout entier. Cette signification profonde en fait une figure essentielle dans la géométrie sacrée.

Représentation dans les traditions anciennes

Dans les civilisations anciennes, le décagone apparaissait souvent dans l'art et l'architecture. Les mosaïques islamiques, par exemple, utilisent fréquemment des motifs décagonaux pour représenter l'infini et la perfection divine. Ces motifs, complexes mais harmonieux, reflètent une compréhension avancée de la géométrie.

Tu peux aussi trouver des traces du décagone dans les temples et les monuments. Les bâtisseurs de l'Antiquité utilisaient cette forme pour concevoir des structures qui inspiraient respect et admiration. Dans certaines cultures, le décagone servait à représenter des concepts spirituels, comme les cycles de la vie ou les lois universelles.

Utilisation dans les motifs géométriques sacrés

Les motifs géométriques sacrés intègrent souvent le décagone pour sa symétrie et son équilibre. Ces motifs, utilisés dans des mandalas ou des vitraux, visent à créer une connexion entre l'esprit et l'univers. En traçant un décagone, tu peux observer comment ses lignes et ses angles forment une base parfaite pour des figures plus complexes, comme les étoiles ou les cercles entrelacés.

Dans la géométrie sacrée, chaque élément du décagone a une signification. Les sommets représentent souvent des points d'énergie ou des étapes dans un chemin spirituel. Les diagonales, quant à elles, symbolisent les connexions invisibles entre ces points. Ces interprétations font du décagone un outil puissant pour la méditation et la contemplation.

Le décagone, avec ses dix côtés et ses nombreuses propriétés géométriques, est une figure fascinante. Tu as découvert sa symétrie, ses angles, et son lien avec le cercle et le nombre d’or. Ces caractéristiques le rendent essentiel en mathématiques, mais aussi en art, en architecture et en sciences.

Plonge dans cet univers et laisse-toi inspirer par la beauté des formes géométriques !

A Propos de Mineral Direct: Mineral Direct – grossiste en minéraux, se spécialise dans la sélection de pierres précieuses et semi-précieuses. Mineral Direct s'engage à offrir des produits de haute qualité. Chaque pierre est soigneusement choisie pour ses propriétés uniques. En l’absence d’intermédiaires, nous minimisons les coûts pour maintenir les prix à  la portée de tous. L'équipe de Mineral Direct partage sa passion pour la lithothérapie. Les experts guident les clients dans leur choix de pierres.  Mineral Direct offre une expérience d'achat unique. Les clients explorent une vaste collection de pierres, bijoux et d'objets en pierres naturelles. L'entreprise s'efforce de rendre chaque achat mémorable. Mineral Direct valorise la satisfaction des clients. Les avis positifs témoignent de la qualité des produits. Mineral Direct inspire confiance et fidélité. L'entreprise continue d'innover pour répondre aux besoins des clients.